comap-o奖论文学习
【ai帮我汇总的prompt】
- 针对每道题 这些文章分别用了哪些模型 给我汇总一个table然后简要介绍这些模型的原
2025 a
模型汇总
好的,我为您梳理了这四篇关于楼梯磨损分析(MCM 问题 A)的报告,它们在解决各个子问题时所采用的核心模型,并简要介绍了其原理。
核心模型汇总表
| 任务(问题) | 团队 2500836 | 团队 2501909 | 团队 2504218 | 团队 2511565 | 团队 2501567 |
|---|---|---|---|---|---|
| 1. 测量磨损与计算使用频率 | Archard 定律 1111 原理:一个经验公式,将材料的磨损体积(或深度)与施加的法向载荷、滑动距离和材料硬度关联起来 2。该报告用它来计算每日的行人流量 3333。 |
WVM (磨损体积模型) 4444 原理:基于 Archard 磨损定律 5555,将总磨损量与楼梯年龄 (T)、使用频率 ( |
混合磨损 PDE 模型 77777 原理:基于 Archard 定律 建立一个偏微分方程 (PDE) 888,将磨损速率 ( |
Delaunay 三角剖分 101010 原理:一种将离散点云数据转换为三角形网格的算法 11。通过计算所有三角形(棱柱)的体积总和,来估算总的磨损体积 12。 Archard 磨损模型 13131313(粘附磨损 14 + 磨料磨损 15) 原理:利用计算出的总磨损体积 (V) 和已知的楼梯年龄 (t),反向求解每日的平均人流量 (n) 16161616。 |
Archard 磨损定律 3 原理:基础物理模型,将磨损体积 ( 线性回归 5555 原理:将总磨损量建模为 |
| 2. 分析行走偏好(方向与并排) | 二维正态分布 17171717 原理:假设磨损凹陷的形状服从二维高斯分布。通过 PSO (粒子群优化) 18181818算法拟合参数,并定义“方向偏好指数”(比较中心与边缘的磨损 19191919)来判断方向。 Navier-Stokes 方程 20202020 原理:将行人流体视为连续介质,使用流体动力学方程建模 21212121。通过有限差分法 22222222求解行人密度 ( |
WDM (磨损分布模型) 24242424 原理:基于中心极限定理 25252525,假设磨损的边际分布服从高斯混合模型 (GMM) 26262626。 • Y轴 (方向): 拟合两个高斯分布,其均值 ( • X轴 (并排): 拟合 k 个高斯分布,峰值的数量 k 即为并排行走的人数 282828282828282828。 |
单人/并排混合模型 292929 原理:将总的脚步分布 ( FPTDM (脚步分区模型) 323232323232323232 原理:假设上楼主要磨损台阶的“前 2/3” ( |
GMM + BIC 模型 35353535 原理:使用高斯混合模型 (GMM) 36363636拟合磨损分布,并使用EM算法 37373737求解。 • Y轴 (方向): 拟合两个高斯分布,其权重 ( • X轴 (并排): 拟合 k 个高斯分布,并通过最小化贝叶斯信息准则 (BIC) 39393939来确定最佳的 k 值(即并排人数) 40。 |
GMM (高斯混合模型) 20202020 原理:假设磨损分布是多个高斯分布的混合体 21212121。 • Y轴 (方向): 拟合两个高斯分布,其权重 ( • X轴 (并排): 拟合 k 个高斯分布 23,并通过最小化BIC (贝叶斯信息准则) 来确定最佳的 k 值(即并排人数) 24242424。 |
| 3. 估算年龄与检测修复 | Monte Carlo (蒙特卡洛) 模拟 4141414141 原理:在已知的磨损-年龄关系式 42中,对参数(如磨损深度、人流量等)进行随机抽样,以估算楼梯年龄的 95% 置信区间 434343434343434343。 化学与粗糙度方法 44444444 原理:通过化学分析(如环氧树脂 45)或比较表面粗糙度 46 来检测修复迹象。 |
Brinell (布氏) 硬度标尺 47474747 原理:一种无损测量材料硬度的方法 48。通过比较每级台阶的硬度 ( KL 散度 (Kullback-Leibler) 51515151 原理:一种测量两个概率分布(磨损模式)之间差异的指标 52。如果两级台阶的磨损分布差异过大,则表明其中一个被修复过 53。 |
贝叶斯反演 (Bayesian Inversion) 545454545454545454 原理:将任务1的 PDE 模型作为“正向模型”。通过贝叶斯框架(P( |
h) |
平滑度检测 (梯度分析) 原理:定义一个“修复检测指数” Archard 磨损系数分析 41414141 原理:计算材料的有效磨损系数 (K),并将其与已知来源的材料进行比较。使用 t-test 或 K-S 检验进行统计比较 |
| 4. 分析典型日使用模式 | 偏微分方程 (PDE) / 脉冲函数 555555555555 原理:通过建立瞬时磨损方程 |
Monte Carlo (蒙特卡洛) 模拟 616161 原理:模拟不同的人流密度(即单人行走 |
离散事件模拟 (DES) 656565 原理:将每个行人的脚步视为一个独立的“到达事件” 66,该过程遵循泊松分布 ( |
峰度 (Kurtosis) 计算 69696969 原理:计算磨损分布的峰度值 70。高峰度(>3,分布更尖锐)意味着“长时低频”使用(脚步集中);低峰度($\le$3,分布更平坦)意味着“短时高频”使用(脚步分散) 71。 |
Chaboche 模型 原理:一种材料疲劳损伤模型 。该报告用它来计算“短时高频”(集中使用)和“长时低频”(分散使用)两种模式下累积的损伤量,发现集中使用会加速磨损 |
2025 c
0 模型 汇总
好的,我为您整理了这9篇报告中针对三个主要任务(问题1、2、3)所使用的核心模型。
下表汇总了每篇报告(按团队编号区分)在解决“奖牌预测”(任务1)、“‘伟大教练’效应”(任务2)和“其他洞察”(任务3)时分别采用了哪些关键模型,并简要介绍了这些模型的原理。
9 篇报告的核心模型汇总表
| 团队编号 | 任务 (问题) | 使用的核心模型 | 模型简要原理 |
|---|---|---|---|
| 2500759 1 | 任务 1 | PCA + LSTM + XGBoost-Bootstrap 2 Wilcoxon 检验 3 SHAP & Spearman 4444 |
PCA (主成分分析) 5:数据降维。 LSTM (长短期记忆网络) 6:捕捉时间序列特征。 XGBoost-Bootstrap 7:一种强大的梯度提升决策树模型,结合 Bootstrap (自举法) 来估计置信区间。 Wilcoxon 检验 (非参数检验) 8:用于检验“零突破”国家的预测概率是否显著。 SHAP & Spearman 9999:用于解释特征(项目)的重要性和相关性。 |
| 任务 2 | DID (差分中的差分模型) 10101010 | 一种准实验方法,通过比较“干预组”(教练变更)和“对照组”(未变更)在干预前后的变化差异,来估计政策(教练)的净效应。 | |
| 任务 3 | (模型复用) | 综合运用 PCA, LSTM, 和 SHAP 分析得出额外见解 11111111。 | |
| 2501869 12 | 任务 1 | Hurdle (跨栏) 模型 13 Tobit (托比特) 模型 14 |
Hurdle 模型 15:一个两阶段模型,专门处理“过多零值”的计数数据。第一阶段(通常是 Logit)预测“是否为0”(能否获奖),第二阶段(如截断泊松)预测“非0”的具体数值(奖牌数)。 Tobit 模型 16:用于处理“删失数据”。它假设存在一个无法观测的“潜在奖牌能力”,当该能力低于0时,观测到的奖牌数即为0。 |
| 任务 2 | 贝叶斯变点检测 17 2SLS (两阶段最小二乘法) 18 |
贝叶斯变点检测 19:一种统计方法,用于在时间序列中识别出数据属性(如均值)发生显著变化的“变点”(即教练上任时间)。 2SLS 20:一种回归方法,用于处理“内生性”问题(即教练和奖牌数可能互相影响)。它通过“工具变量”来估算教练的纯粹因果贡献。 |
|
| 任务 3 | (模型复用) | 重新使用贝叶斯变点检测和 Hurdle/Tobit 模型进行深入分析 21。 | |
| 2503389 22 | 任务 1 | MLR-FNN 混合模型 23 Logistic 回归-随机森林混合 24 SIAMOS (自定义模型) 25 |
MLR-FNN 26:融合了“多元线性回归”(MLR) 的可解释性和“前馈神经网络”(FNN) 捕捉非线性关系的能力。 Logistic 回归-随机森林 27:结合了 Logistic 的概率输出和随机森林的分类鲁棒性,用于预测“零突破”国家。 SIAMOS 28:作者自定义的“奥林匹克运动战略重要性评估模型”,通过加权指标评估项目重要性。 |
| 任务 2 | 断点回归 (Breakpoint Regression) 29292929 | 一种准实验方法,通过比较教练上任时间点(断点)前后的数据趋势变化,来量化“伟大教练”的贡献。 | |
| 任务 3 | (洞察分析) | 提出了“东道国溢出效应”,未构建新模型 30。 | |
| 2505964 31 | 任务 1 | Random Forest (随机森林) 32323232 Monte Carlo (蒙特卡洛) 模拟 33333333 |
随机森林 3434:一种集成学习模型,通过构建大量的决策树并取其平均(回归)或投票(分类)结果来进行预测。用于预测运动员的获奖(分类)和能力(回归)。 蒙特卡洛模拟 3535:利用随机森林输出的“概率”,通过大量随机抽样来模拟奖牌(金、银、铜)的具体分配过程,并量化不确定性 36。 |
| 任务 2 | 自定义“伟大教练模型” 37373737 | 作者自定义了一个数学公式 383838383838383838,通过比较教练上任后的实际奖牌数和上任前的“平均运动员能力” 39 来计算教练的贡献值。 | |
| 任务 3 | Poisson (泊松) 回归 404040 Linear Regression (线性回归) 414141 |
泊松回归 42:一种用于“计数数据”(如奖牌数)的回归模型,分析项目数量(自变量)和奖牌数(因变量)之间的关系。 线性回归 43:用于量化“东道国效应” 44。 |
|
| 2507817 45 | 任务 1 | GSRF (网格搜索-随机森林) 464646 Logistic 回归 474747 |
GSRF 48:即带有“网格搜索”调参的随机森林模型,用于预测奖牌数。 Logistic 回归 49:用于“零突破”国家的二元分类问题(预测获奖或不获奖)50。 |
| 任务 2 | Lasso 回归 515151 Spearman 相关性 525252 |
Lasso 回归 53:一种使用 L1 正则化的线性回归。它会自动将不重要的特征(变量)的系数压缩到 0,从而筛选出最有影响力的因素 54。 Spearman 相关性 55:用于验证教练效应和分数之间是否存在显著的非线性关联。 |
|
| 任务 3 | (洞察分析) | 分析了“东道国效应”和“天才运动员”,未构建新模型 56。 | |
| 2510006 57 | 任务 1 | ARIMA + 随机森林 + 线性回归 58 Monte Carlo (蒙特卡洛) 模拟 59 Poisson (泊松) 分布 606060 |
ARIMA 61:一种经典的时间序列模型,用于捕捉数据中的趋势和周期性,预测非“零突破”国家 62。 随机森林 63:用于计算置信区间 64。 蒙特卡洛模拟 65:用于预测“新项目”的奖牌分布 66。 泊松分布 67:用于为“零突破”国家的预测结果计算置信区间 68。 |
| 任务 2 | Fisher's 精确检验 69696969 | 一种用于 2x2 列联表(例如:[教练变更/未变更] vs [获奖/未获奖])的统计检验,用于确定教练变更和获奖之间是否存在显著关联。 | |
| 任务 3 | (相关性分析) | 分析了 GDP 和奖牌数之间的相关性 70707070。 | |
| 2510185 71 | 任务 1 | Random Forest (随机森林) 727272 BP 神经网络分类器 737373 |
随机森林 74:使用网格搜索 (GridSearchCV) 75和自举法 (Bootstrap) 76来预测奖牌数和置信区间。 BP 神经网络 77:一种使用“误差反向传播”(Backpropagation) 算法训练的神经网络,用于“零突破”国家的二元分类任务 78。 |
| 任务 2 | Random Forest (随机森林) 79 自定义“EPI”模型 80 |
随机森林 81:通过在特征中加入“有无伟大教练”的二元变量,来预测奖牌变化,从而量化教练的贡献 82828282。 EPI (事件潜力指数) 83:作者自定义的加权公式 84,用于评估哪些项目最值得投资教练。 |
|
| 任务 3 | (模型复用) | 基于随机森林的“特征重要性” 85和 BP 神经网络的预测结果 86 提出见解。 | |
| 2510862 87 | 任务 1 | Stacking 集成模型 888888 Bootstrap (自举法) 898989 |
Stacking 集成 90:一种高级集成方法。它使用多个“基础模型”(如 LGBM, SVM, XGBoost 等)的预测结果作为“元学习器”(如逻辑回归)91的输入,来进行最终预测。 Bootstrap 92:通过数据重采样来估计 95% 置信区间 93。 |
| 任务 2 | PSM-DID 模型 949494 K-Means 聚类 959595 |
PSM-DID 96:“倾向得分匹配”(PSM) 97是一种统计方法,用于在“干预组”和“对照组”中找到特征相似的样本对,然后再使用 DID 模型进行因果推断。 K-Means 聚类 98:一种无监督算法,用于将国家按“潜力”和“近期表现” 99 分群,以找出适合投资的国家。 |
|
| 任务 3 | Pearson 相关性 & SHAP 100100 | Pearson 相关性 101:衡量项目和奖牌数之间的线性相关程度。 SHAP 102:用于解释 Stacking 模型,找出哪些项目对美国队的奖牌贡献最大 103。 |
|
| 2514362 104 | 任务 1 | 混合效应负二项回归 105105105 ZINB (零膨胀负二项) 106106106 |
混合效应负二项回归 107:一种高级回归模型。“负二项”用于处理方差大于均值(过离散)的计数数据(奖牌数);“混合效应”用于同时考虑固定效应(如历史成绩)和随机效应(如国家异质性)108。 ZINB 109:一种处理“过多零值”的模型。它假设零值来自两个过程:一是“真零”(国家有能力但没获奖),二_是_“结构性零”(国家根本没能力获奖)110。 |
| 任务 2 | 贝叶斯修正的熵模型 111111111111 | 一种基于信息论的模型。“熵”用来衡量不确定性,“信息增益 (IG)” 112112112112用来量化教练的引入(作为一种信息)对减少“奖牌不确定性”的贡献。使用了“拉普拉斯平滑” 113113113113 来处理小样本数据。 | |
| 任务 3 | (模型复用) | 基于 ZINB 和熵模型的结果提出见解(如“潜在奖牌”)114。 |
1. 2025 c 2503389
这篇还是很有说法的,因为它的图其实都挺丑的,可见思路的创新,深刻有时候也是关键


感觉模型多是基础
2. 2025c-2505964
关键图!!!!!

学习一下

3. 2025c-2507817
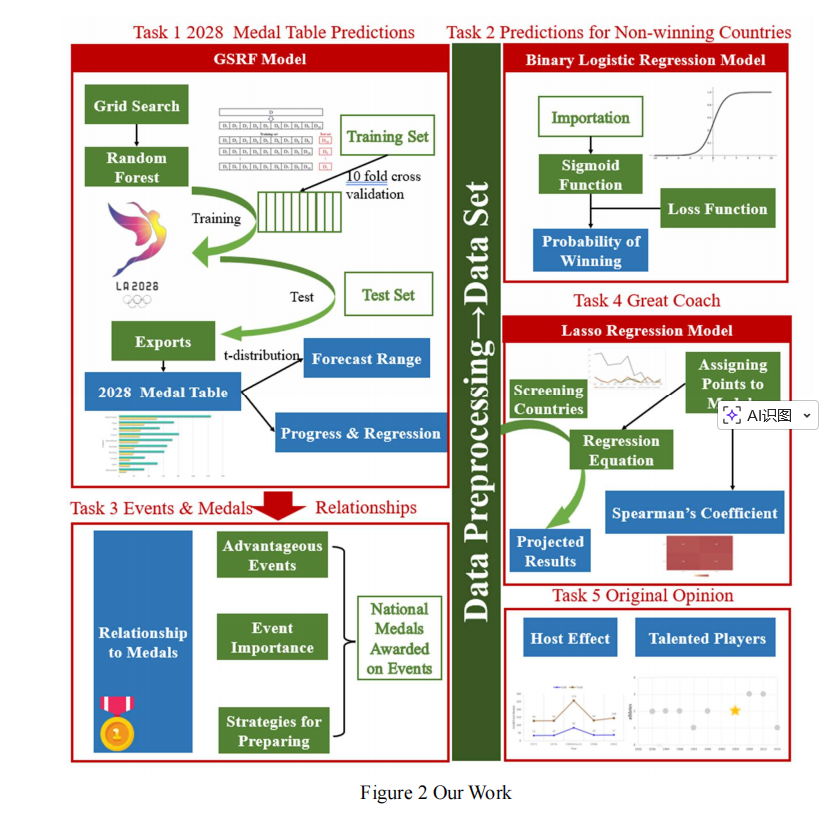
比较次要
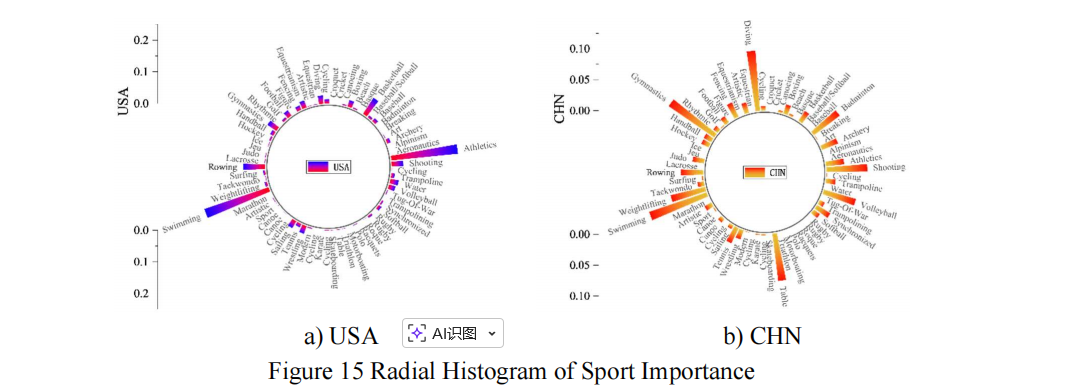
简单有效
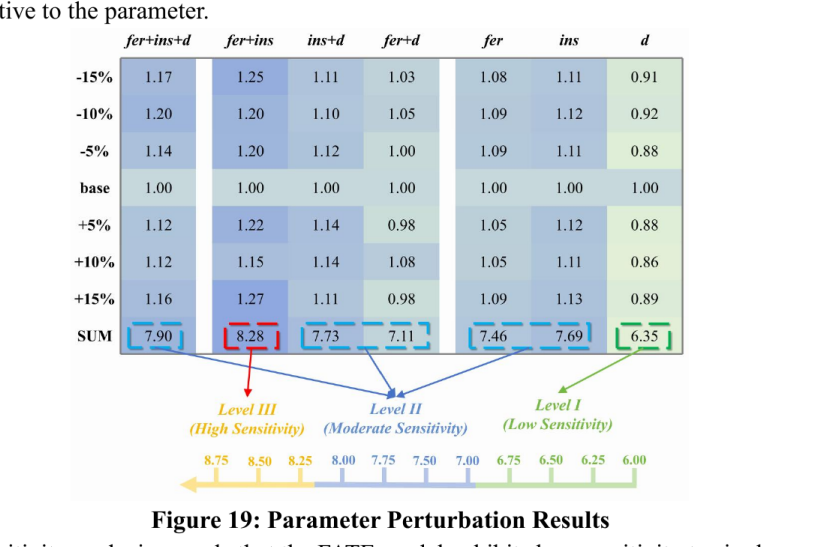
比较高级没看懂
2025c-2510006
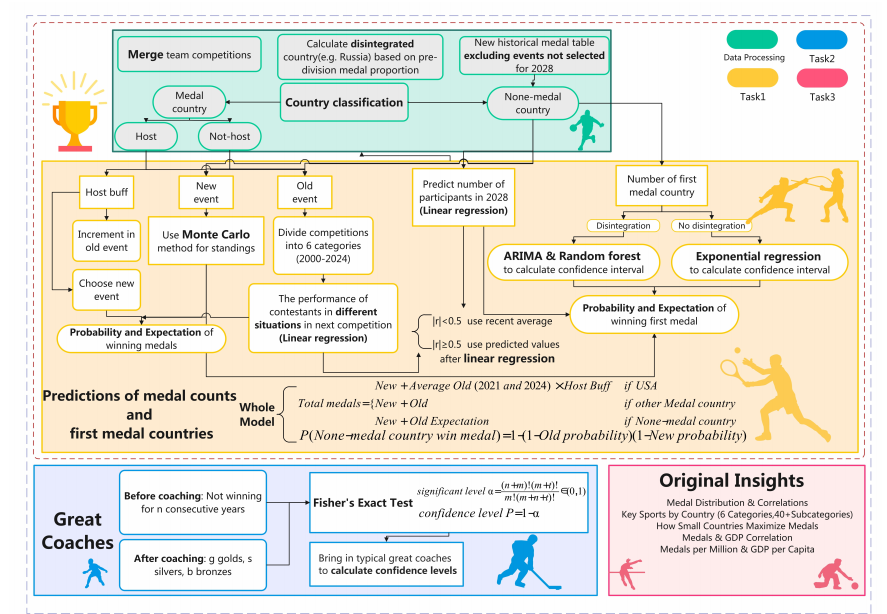
2025-E
好的,这是一个关于生态农业建模(MCM 问题 E)的请求。我为您梳理了这三篇报告(2515136、2502355、2508861)在解决不同任务时所使用的核心模型,并汇总在下表中。
这三篇报告都遵循了竞赛题目的要求,大体上分为四个任务:
-
任务 1: 建立一个农业生态系统的食物网模型。
-
任务 2: 分析物种回归(如狐狸、猞猁等)对生态系统的影响。
-
任务 3: 分析移除除草剂和引入有益物种(如蝙蝠、蜜蜂等)的影响。
-
任务 4: 评估不同有机农业(Organic Farming)方案的综合效益。
核心模型汇总表
| 团队编号 | 任务 | 使用的核心模型 | 模型简要原理 |
|---|---|---|---|
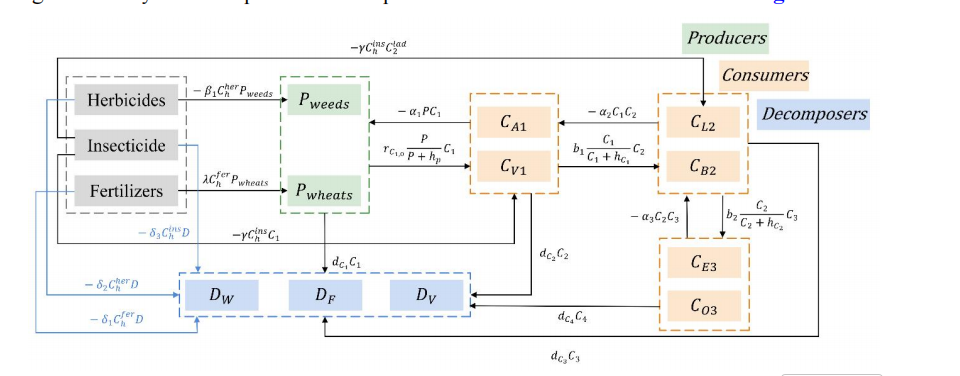
| 2515136 | 任务 1 | PFW (Petri-Food Web) 模型 1 | 基于皮特里网 (Petri nets) 2222、Lotka-Volterra 理论 333和能量流理论 4建立。使用能量而非种群数量作为分析单位 5,并用龙格-库塔 (Runge-Kutta) 算法求解 6666。 |
| 任务 2 | PFW 模型扩展 77 + 生态系统成熟度指数 ( |
在 PFW 模型中加入红狐 (red fox) 和猞猁 (lynx) 9999。同时定义了一个包含物种丰富度、生物量、P/R比率等的生态系统成熟度指数 10101010,用于量化稳定性。 | |
| 任务 3 | HRP (除草剂移除预测) 模型 11 | 扩展 PFW 模型,引入了基于 Lotka-Volterra 的小麦-杂草竞争关系 12121212。通过对比引入蝙蝠 (bats) 和啄木鸟 (woodpeckers) 后的成熟度指数来评估其影响 13131313。 | |
| 任务 4 | OAIE (有机农业影响评估) 模型 1414 | 这是一个多级模糊综合评价模型 15151515。该模型选取了生态系统、作物生长等4个一级指标和10个二级指标 16161616,并使用熵权法 (EWM) 来计算权重 17171717。 | |
| 2502355 | 任务 1 | 常微分方程组 (ODE) 模型 181818 | 使用微分方程 19逐步建立模型。从简单的三营养级食物链 20202020(使用 Holling-II 型功能性反应 21) 扩展到包含土壤和分解者的食物网 22222222(使用 Holling-I 型功能性反应 23),最后引入农业周期和季节性因素 24242424。 |
| 任务 2 | 网络理论 (Graph Theory) 模型 25 | 将生态系统构建为网络图 26。使用任务1中计算出的碳流量 (Carbon flow) 27作为边的权重,通过计算“稳定性”、“生物多样性”和“中心性”指标 28 来评估引入新物种(狐狸和猞猁)后的变化。 | |
| 任务 3 | 网络理论模型 (续) | 继续使用网络理论模型,通过移除化学品和引入蝙蝠 (bats) 或蜜蜂 (bees) 来构建不同的网络情景 29292929,并计算对比其稳定性 30、多样性(香农-维纳指数)31和中心性(特征向量中心性)32323232 指标。 | |
| 任务 4 | EWM-AHP (熵权法-层次分析法) 模型 333333 | 提出三种有机农业措施(改良土壤、害虫管理、人工除草)并进行组合 34343434。使用 EWM (熵权法) 35获取客观权重,并(隐含地)结合 AHP (层次分析法) 36 的结构来对不同方案进行综合评分和排序。 | |
| 2508861 | 任务 1 | FATE (森林到农业过渡生态系统) 模型 37373737 | 结合 Lotka-Volterra 模型 和 广义 Logistic 模型 38383838。创新点在于引入了空间扩散项 (Spatial Diffusion Term) 39393939 (即偏微分方程, PDE),并用有限体积法 (FVM) 40求解,同时考虑了农业周期和季节性 41414141。 |
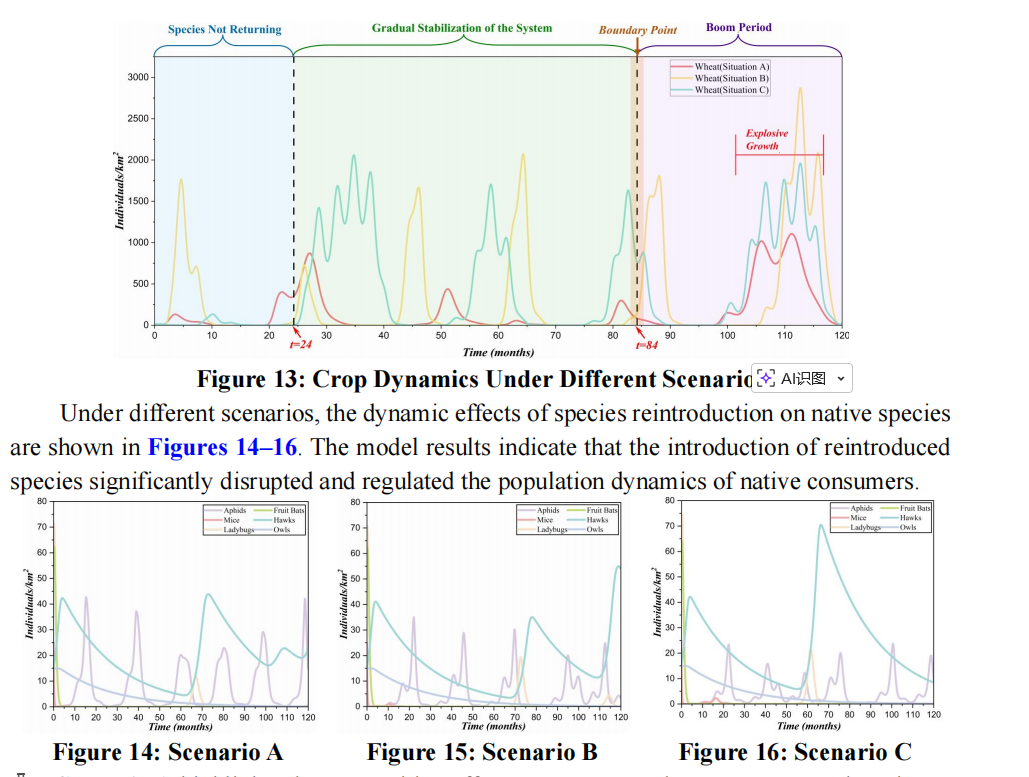
| 任务 2 | SDM (物种分布模型) 42 + 多情景模拟 43 | 使用 GLM (广义线性模型) 或 GAM (广义相加模型) 44来预测物种(蜜蜂、云雀、灌木)回归的概率。然后将这些物种的回归组合(A, B, C三种情景)45 代入 FATE 模型中进行模拟,以评估其影响。 | |
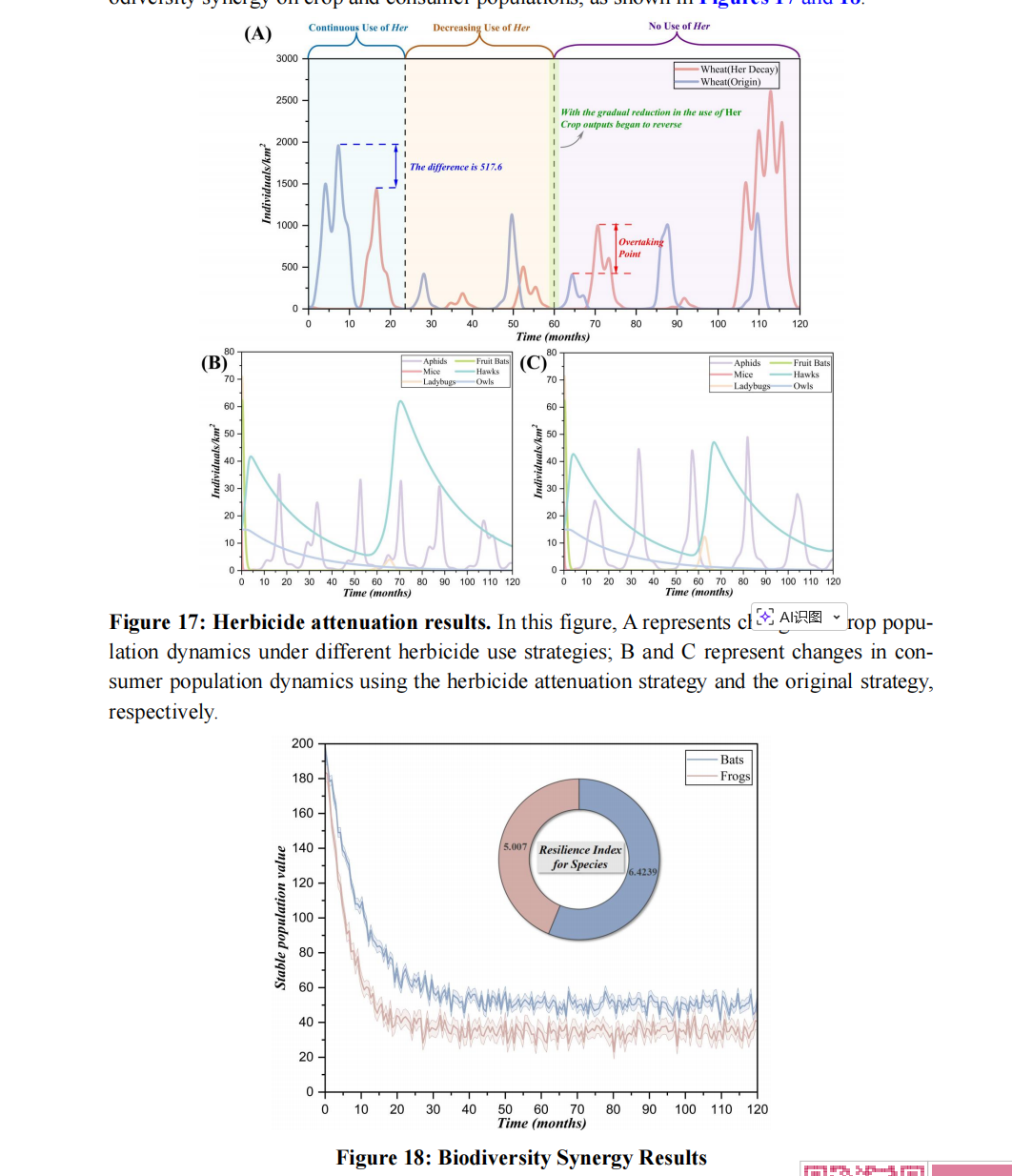
| 任务 3 | FATE 模型扩展 46 + 系统恢复力指数 (Resilience Index) 474747 | 在 FATE 模型中引入“除草剂依赖性降低”的时间函数 48。通过对比引入蝙蝠 (bats) 和青蛙 (frogs) 49494949后的系统恢复力指数 (R) 50 来评估不同物种的效果。 | |
| 任务 4 | COMAP (综合有机管理与规划) 模型 515151 | 这是一个多目标非线性规划模型 52,用于权衡“生态效益”和“经济效益”两大目标 535353。作者证明了模型是凹的 (concave) 54545454,并使用凸重构法 (Convex Reformulation) 55、拉格朗日对偶和 e-约束法 56565656 求解。 |
E-2508861
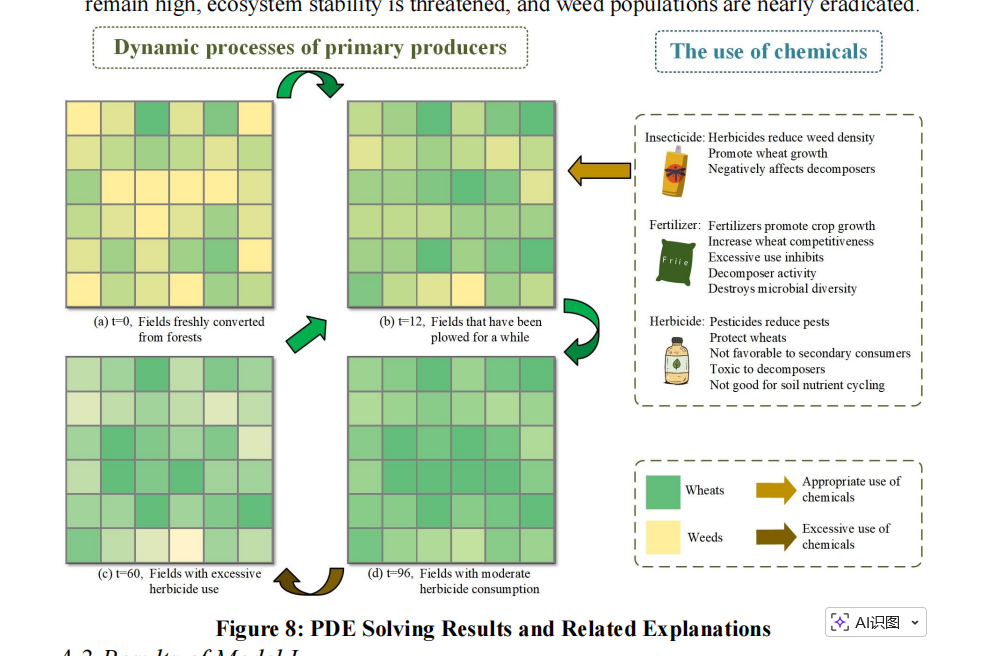

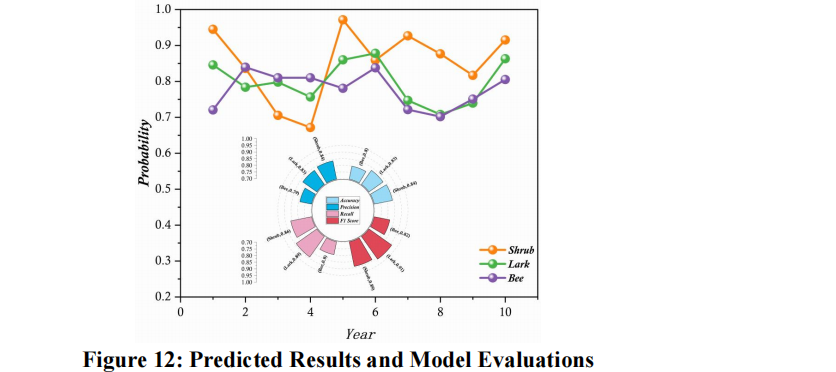
至少10张绝顶的图